MICROTOPS
- Ogólne warunki synoptyczne w czasie
trwania INDOEX-u.
Eksperyment INDOEX
byl prowadzony w pólnocnej czesci Oceanu
Indyjskiego
w czasie trwania monsunu
zimowego. W skutek tego warunki meteorologiczne byly w tym
rejonie dosc stabilne. Na pólkuli poludniowej po nizej 15
równoleznika wystepowaly bardzo stale pasaty poludniowo
wschodnie siegajace srodkowej troposfery. Glównym osrodkiem
barycznym ksztaltujacym pogode w tej czesci byl Wyz
Poludniowoindyjski z centrum okolo 30 równoleznika. W tym obszarze transport aerozolu odbywal sie z
centralnej czesci Oceanu Indyjskiego, gdzie nie wystepuja zródla
zanieczyszczen. Zwiazku z tym w rozwazanym obszarze nalezy
spodziewac sie malych grubosci optycznych aerozolu. Pomiedzy 5 a
10 stopniem szerokosci geograficznej
poludniowej znajdowala sie strefa zbieznosci (ITCZ
–intertropical convergence zone). Jej polozenie ulegalo
zmiana jednak rzadko wykraczalo poza ten obszar. Strefa
zbieznosci znajdowala sie w strefie szerokiej bruzdy niskiego
cisnienia. Ze wzgledu na
zbieznosc wiatru w dolnej troposferze dochodzi w tym regionie do
kumulacji aerozolu pochodzacych z obu pólkul. Dzieki tej strefie
duze ilosc zanieczyszczen pochodzacych z pólkuli nie moga
przemieszczac sie swobodnie daleko na pólkuli poludniowej. W
obszarze równikowych w
dolnej troposferze dominowaly wiatry slabe wiatry zachodnie, zas
w rejonie tropopauzy wiatry wschodnie i poludniowo wschodnie. Na
pólkuli pólnocnej glówne osrodki baryczne to wyz w rejonie
Pólwyspu Arabskiego, plytki niz nad poludniowa czescia Pólwyspu Indyjskiego, ponadto
rozlegly niz znad poludniowych Chin oraz klin wyzowy nad Zatoka
Bengalska. W skutek tego w rejonie Morza Arabskiego wystepowaly
stale wiatry pólnocno wschodnie transportujace ogromne ilosci
zanieczyszczen w kierunku równika. Dalej na poludnie wiatr w obszarze
równikowym skrecal w lewo i przyjmowal kierunek zachodni jeszcze
na pólkuli poludniowej a nie jednokrotnie jeszcze na pólkuli
pólnocnej. Ze wzgledu na wiatry zachodnie w tym obszarze, strefa
ITCZ od 55 stopnia dlugosci geograficznej na wschód nie
otrzymywala duzej ilosci aerozoli. W rejonie Zatoki Bengalskiej
wiatry maily taki sam kierunek jak na Morzu Arabskim. Na poziomie
700 mb w obszarze Pólwyspu Indyskiego cyrkulacja cyklonalna
powodowala transport aerozolu znad srodkowych Indii na zachód w poludniowe
rejony Morza arabskiego.
2. Microtops
Jednym z przyrzadów do pomiarów
grubosci optycznej jest microtops. Pomiary odbywaja sie w pieciu
kanalach, pierwsze trzy znajduja sie w obszarze widzialnym (440,
500 675 nm), zas dwa kolejne w bliskiej podczerwieni (870,
936nm). Ostatni kanal pomiarowy znajduje sie w obszarze silnego
pochlaniania przez pare wodna co daje mozliwosc pomiaru
calkowitej zawartosci pary wodnej w pionowej kolumnie powietrza.
Przyrzad wspólpracuje z systemem
GPS co umozliwia wykonywanie pomiarów w ruchu np. na statku czy
z samolotu. Microtops mierzy równiez natezenie bezposredniego
promieniowania slonecznego w wyzej wspomnianych pasmach. Jest to
przyrzad wymagajacy recznego ustawiania na slonce. Pojedynczy pomiar trwa 10 sekund w czasie
których microtops dokonuje pomiaru poziomu sygnalu we wszystkich
kanalach. Sygnal wyjsciowy jest proporcjonalny do natezenia
promieniowania bezposredniego dochodzacego do detektora.
- Przejscie
promieniowania slonecznego
przez atmosfere.
- Rozpatrzmy przejscie
promieniowania slonecznego przez atmosfere.
Natezenie promieniowania bezposredniego wyraza
sie wzorem Beer'a:
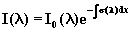 (3.1.1)
(3.1.1)
gdzie: s (l ) jest wspólczynnikiem
eksynkcji, zas I0 natezeniem promieniowania
poza atmosfera.
Powyzszy wzór
mozna zapisac przy pomocy grubosci optycznej
atmosfery t w nastepujacej postaci:
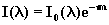 (3.1.2)
(3.1.2)
gdzie m jest masa
optyczna atmosfery.
W czasie
przechodzenia promieniowania przez atmosfere
nastepuje jego absorbcja oraz rozpraszanie. Dla
zakresu dlugosci fal mierzonych przez microtopsa
zasadnicze znaczenie maja nastepujace procesy:
rozpraszanie molekularne, rozpraszanie po przez
aerozole zawarte w powietrzu, absorbcja przez
ozon oraz pare wodna. Ostatni proces odbywa sie w
dla dlugosci fali rejestrowanej w ostatnim kanale
przyrzadu (936 nm).
Calkowita grubosc
optyczna wyraza sie wiec wzorem:
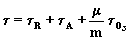 (3.1.3)
(3.1.3)
gdzie; 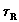 ,
, 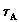 ,
, 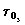 oznaczaja odpowiednio
grubosc optyczna: molekularna, aerozolowa oraz
ozonowa.
oznaczaja odpowiednio
grubosc optyczna: molekularna, aerozolowa oraz
ozonowa.
W przypadku
dlugosci fali 936 nm grubosc optyczna przyjmuje
postac:
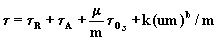 (3.1.4)
(3.1.4)
gdzie: k, b sa
stalymi zaleznymi od charakterystyki filtru.
- Masa optyczna atmosfery i
ozonu.
Masa optyczna jest wielkoscia
okreslajaca liczbie atmosfer przez jakie przechodzi
promieniowanie sloneczne. Jest ona funkcja kata azymutalnego i
równa z definicji jednosci gdy slonce znajduje sie w zenicie.
Wielkosc ta jest wiec proporcjonalna do liczby czasteczek
powietrza bedacych na drodze promieniowania. Przy zalozeniu
stalego skladu chemicznego atmosfery
(stalosc masy molowej powietrza) masa optyczna jest równa
stosunkowi masy powietrza bedacej w slupie atmosfery obejmujacym
bezposrednie promieniowanie sloneczne do masy powietrza w
pionowym slupie.
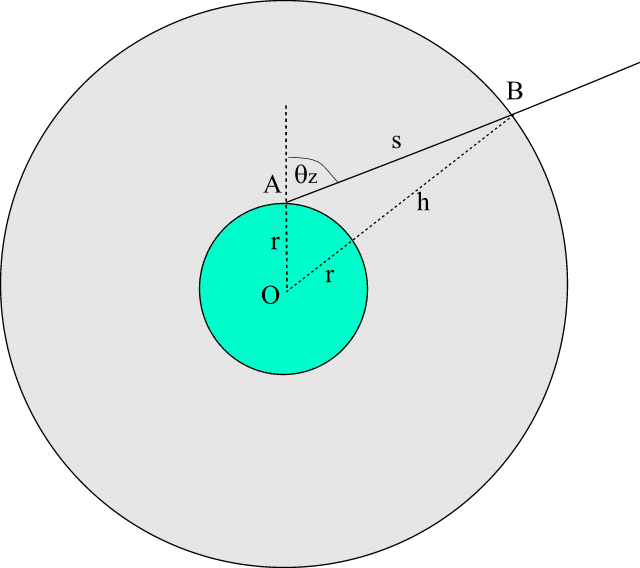
Rys. 1 Droga
promieniowania slonecznego w atmosferze.
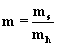 (3.2.1)
(3.2.1)
Masa powietrza wyraza sie wzorem:
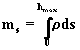 (3.2.2)
(3.2.2)
Uwzgledniajac wzór barometryczny
mamy:
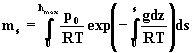 (3.2.3)
(3.2.3)
Przyjmujac, ze temperatura
atmosfery jest stala wzór upraszcza sie do postaci:
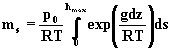 (3.2.4)
(3.2.4)
W celu wyznaczenia wielkosci ms
trzeba znalezc relacje
pomiedzy wielkoscia a wysokoscia nad poziom morza h. W tym celu
korzystamy z tw. cosinusów dla trójkata ABO (rys 1) i
otrzymujemy:
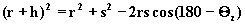 (3.2.5)
(3.2.5)
Rozwiazujac równanie ze wzgledu
na zmienna h mamy:
 (3.2.6)
(3.2.6)
Podstawiajac do wzoru 3.2.4 mamy:
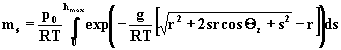 (3.2.7)
(3.2.7)
Masa powietrza jednostkowego
pionowego slupa atmosfery przy zalozeniu stalej temperatury
wynosi:
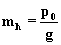 (3.2.8)
(3.2.8)
Ostatecznie po podstawieniu do wzoru
3.2.1 otrzymujemy poszukiwany zwiazek:
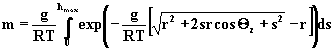 (3.2.9)
(3.2.9)
Powyzsze wyrazenie pod calka nie
daje sie analitycznie odcalkowac mozna jedynie uprosc problem
rozwijajac wyrazenie pod pierwiastkiem ze wzgledu na relacje
r>>s. W rezultacie po scalkowaniu otrzymuje sie dobrze
znany wzór:
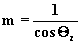 (3.2.10)
(3.2.10)
Wzór ten jest dokladnie masa
optyczna przy zalozeniu, ze powierzchnia ziemi jest plaska.
Wynika z tego zakres stosowalnosc dla duzych katów zenitalnych.
Generalnie wzór 3.2.10 jest poprawny, gdy kat zenitalny slonca
jest mniejszy od 600.
Wygodniej zamiast zwiazku 3.2.10
uzyc wzorów empirycznych do obliczania masy optycznej atmosfery.
Jednym z takich wzorów jest formula Kasten’a:
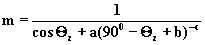 (3.2.11)
(3.2.11)
gdzie: a=0.50572, b=6.079950, c=1.6364
Przebieg zmiennosc masy optycznej
w zaleznosci od kata zenitalnego przedstawiony jest na wykresie
3.2.1. Wynika z niego, ze gdy slonce znajduje sie nisko nad
horyzonetm masa optyczna zmienia sie bardzo szybko. W czasie
zachodu slonca wynosi 38 oznacza to, ze tylez samo razy wiecej
oslabiane jest promieniowanie sloneczne w czasie zachodu w
stosunku oslabienia, gdy znajduje sie ono w zenicie.
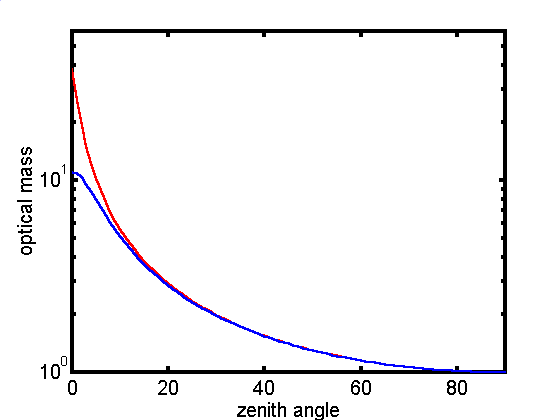
Wyk. 3.2.1 Masa
optyczna atmosfery (czerwona linia) i masa optyczna ozonu
(niebieska linia) w zaleznosci od kata azymutalnego.
Podobna wielkosci
do masy optycznej atmosfery jest masa optyczna ozonu. Rózni sie
ona jedynie tym ze pod uwage nie bierzemy wszystkich gazów
atmosferycznych o jedynie ozon. W przypadku gdyby cisnienie ozonu
zmienialo sie wg wzoru barometrycznego obie wielkosci bylyby
równe. Jednak ozon zawarty jest glownie w stratosferze dlatego
masa optyczna ozonu ze wzgledu na krzywizne powierzchni ziemi bedzie
inna. W celu jej obliczenia rozwazmy przejscie promieniowania
bezposredniego przez atmosfere i zalózmy, ze gestosc ozonu w
warstwie ozonowej jest stala. Wówczas masa optyczna ozonu jest
równa stosunkowi drogi jaka pokonuje promieniowanie
sloneczne w ozonosferze, gdy
slonce tworzy kat zenitalny 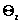 do drogi promieniowania w czasie gdy slonce jest w zenicie. Zgodnie
z oznaczeniami na rys.1 mamy:
do drogi promieniowania w czasie gdy slonce jest w zenicie. Zgodnie
z oznaczeniami na rys.1 mamy:
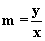 (3.2.12)
(3.2.12)
Stosujac tw. cosinusów dla
trójkatów: ACO oraz AB0 otrzymujemy uklad równan:
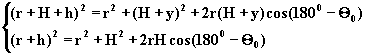 (3.2.13)
(3.2.13)
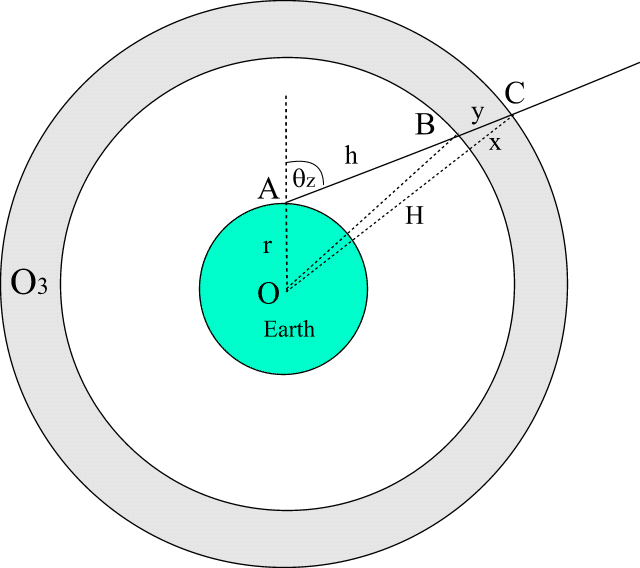
Rys. 2 Droga promieniowania w ozonosferze.
Podstawiajac ze wzoru 3.2.13 za y
rozwiazujemy pierwsze równanie ze wzgledu na zmienna H+y.
W rezultacie otrzymujemy równanie:
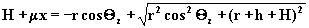 (3.2.14)
(3.2.14)
Drugie równanie rozwiazujemy ze
wzgledu na zmienna H co prowadzi do wzoru:
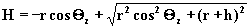 (3.2.15)
(3.2.15)
Podstawiajac za H z równania
3.2.15 do wzoru 3.2.12 dostajemy:
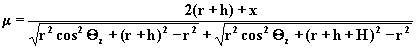 (3.2.16)
(3.2.16)
przyjmujac zalozenie
x<<(R+h) otrzymujemy koncowy wzór:
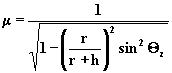 (3.2.17)
(3.2.17)
Masa optyczna ozonu zalezy od
wysokosci dolnej granicy ozonosfery. Poziom ten mozna obliczyc ze
wzoru:
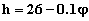 [km] (3.2.18)
[km] (3.2.18)
gdzie 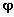 jest szerokoscia geograficzna w stopniach
jest szerokoscia geograficzna w stopniach
Z wykresu 3.2.1 wynika, ze masa
optyczna ozonu i atmosfery sa prawie równe dla kata zenitalnego
mniejszego od 700.
Dopiero gdy slonce znajduje sie nisko nad horyzonetm obie
wielkosc znacznie sie róznia. Podczas zachodu slonca masa
optyczna ozonu wynosi tylko 11.
3.3 Molekularna
grubosc optyczna.
Promieniowanie sloneczne
przechodza przez atmosfere ulega rozpraszaniu na czasteczkach
znaczniej mniejszych od dlugosci fali. Rozpraszanie to jest
czasowo niezmiennicze wobec czego grubosc optyczna jest stala.
Wartosc jej mozna policzyc ze wzoru Deschamps’a:
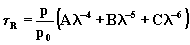 (3.3.1)
(3.3.1)
gdzie: A=84.3510-4 m m-4,
B=-1.22510-4 m m-5
, C=1.410-4 m m-5
Rayleighowska grubosc optyczna
zalezy liniowo od cisnienia atmosferycznego (grubosci atmosfery).
Jest ona malejaca funkcja dlugosci fali. W pierwszym kanale
pomiarowym microtopsa wynosi 0.25, jest to wartosc porównywalna
z gruboscia optyczna aerozolu. W bliskiej podczerwieni
molekularna grubosc optyczna jest mniejsza od 0.05 (wyk …)
- Grubosc
optyczna ozonu.
Grubosc optyczna
ozonu wyraza sie wzorem:
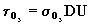 (3.4.1)
(3.4.1)
gdzie 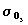 jest ekstynkcja ozonu, DU oznacza
calkowita zawartosc ozonu w Dobsonach
jest ekstynkcja ozonu, DU oznacza
calkowita zawartosc ozonu w Dobsonach
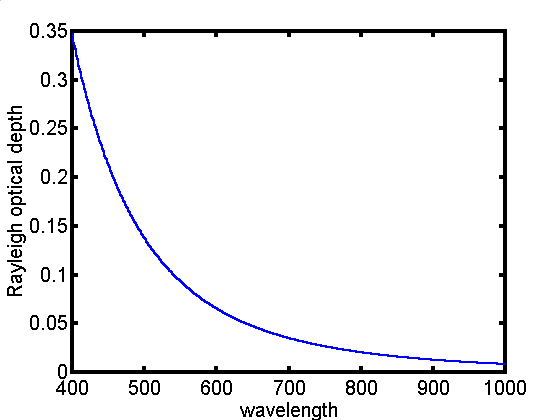
Wyk 3.3.1
Molekularna grubosc optyczna jako funkcja dlugosci fali
Grubosc optyczna ozonu dla DU=300
przedstawiona jest na wykresie 3.3.1 obejmujacym jedynie zakres
widmowy mierzony przez microtopsa. Maksimum wspólczynnika
ekstynkcji a zarazem grubosci optycznej w tym przypadku przypada
na fale o dlugosci okolo 600 nm. W zasadzie niezerowy przyczynek
do calkowitej grubosci optycznej wystepuje tylko w dwóch
kanalach (500 i 675 nm). Grubosc optyczna w tych obszarach
widmowych wynosi okolo 0.01.
3.5 Grubosc optyczna
pary wodnej
Istotny wplyw na calkowita
grubosc optyczna dla fal od dlugosci 936 nm ma para wodna.
Oslabienie promieniowania dla tych dlugosci fali jest silnie
zalezne od calkowitej zawartosci pary wodnej w atmosferze. W
obszarach tropikalnych, gdzie typowa grubosci pary wodnej wynosi
3 cm oslabienie promieniowania wynosi od 70-80%.
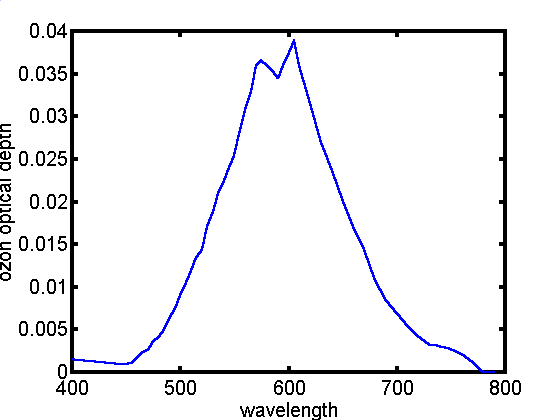
Wyk 3.1.1 Grubosc
optyczna ozonu dla DU=300 w funkcji dlugosci fali.
4. Grubosc optyczna
na pólnocnej czesci Oceanu Indyjskiego – wyniki z microtopsa.
W czasie trwania eksperymentu
INDOEX pomiary grubosci optycznej byly prowadzone w okresie od 57
do 89 julian day. Podczas pierwszego etapu wykonywano pomiary
pomiedzy 11.5 stopniem szerokosc poludniowej o 4 równoleznikiem
pólkuli pólnocnej w czasie kolejnych pieciu dni ( 55, 56, 57,
58, 59 jd). Wszystkie dane z przyrzadu sa poprawne jedynie
struktura danych dwóch pierwszych dni jest inna. Drugi etap
zaczal sie 63 jd i trwal 18 dni. Pomiary prowadzone byly pomiedzy
18 równoleznikiem pólkuli pólnocnej a 10 stopniem szerokosci poludniowej w
nastepujacych dniach: 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73,
74, 75, 76, 78, 79, 80 jd. W okresie od 66 do 69 jd oraz 78
system GPS nie dzialal poprawnie co sprawilo, ze dane z tego
okresu sa zle. W czasie ostatniego
etapu zgromadzone zostaly dane z nastepujacych dni: 85, 86, 88,
89 jd. Wszystkie dane z tego okresu sa dobre i nadaja sie
do dalszej analizy.
Podczas INDOEX-u przeprowadzono
dwa razy kalibracje przyrzadu metoda Langley'a, na poczatku
eksperymentu (57 jd) oraz na koncu (89 jd) w celu sprawdzenia
porównywalnosci danych.
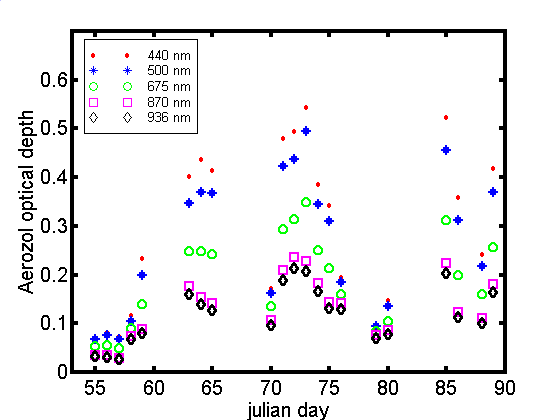
Wyk. 4.1 Grubosc
optyczna aerozolu dla pieciu dlugosci fali w zaleznosci od julian
day
Grubosc optyczna aerozolu -AOT
(aerosol optical thicknes) w czasie pierwszego etapu badan byla
zdecydowanie najmniejsza. W pierwszych trzech dniach (55-57 jd)
byla mniejsza 0.1 we wszystkich kanalach i wynosila okolo 0.08
dla 500nm. W nastepnych dniach (58-59 jd) nastapil znaczny wzrost
AOT do wartosci 0.2 (500nm). W tym czasie statek przeplywal przez
strefe zbieznosci (ITCZ) zlokalizowana pomiedzy 2-4 stopniem
szerokosci geograficznej poludniowej w kierunku pólnocno
wschodnim. Po przekroczeniu ITCZ grubosc optyczna nie zmalala
lecz przeciwnie nastapil dalszy jej wzrost. Przyczyniaja sie do
tego zachodnie wiatry w
strefie okolo równikowej, które nie transportuja zanieczyszczen
z pólkuli pólnocnej dalej na poludnie.
Wykladnik Angstroma podobnie jak
grubosc optyczna aerozolu rosnie w kierunku pólnocnym. W
obszarze 10 równoleznika pólkuli poludniowej wynosi okolo 1.1,
zas na pólkuli pólnocnej w obszarze 4 stopnia wynosi 1.4.
Oznacza to, ze koncentracja malych czastek rosnie w miare
przesuwania sie na pólnoc. Jedynie 58 jd obserwowane bylo
znaczne zmniejszenie sie wykladnika Angstroma do wartosci 0.7 co bylo spowodowane obecnoscia chmur ci
subvisual w obszarze ITCZ.
W drugim etapie badan grubosc
optyczna aerozolu poczatkowo byla duza (0.4 dla 500nm) ale
wartosc jej szybko malala jak statek plynal na pólnoc. W
srodkowej czesci Morza Arabskiego wynosila juz tylko 0.16
(500nm). Jednoczesnie szybko obnizal sie wykladnik Angstroma co
swiadczy o zmniejszaniu sie zawartosci malych aerozoli w
powietrzu. Na 15 równolezniku wynosil on 0.8 co sugeruje, ze w
powietrzu znajdowalo sie stosunkowo niewiele zanieczyszczen pochodzenia antropogenicznego.
Polozenie tego
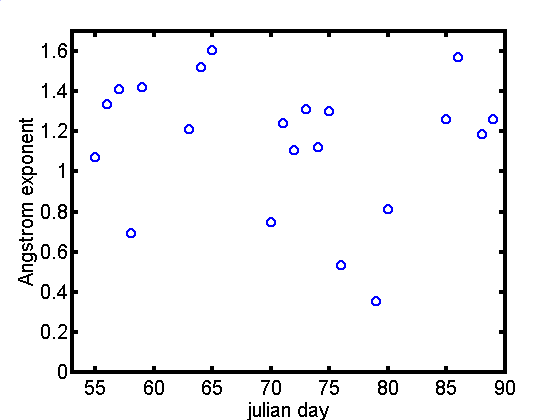
Wyk. 4.2 Wartosc
wykladnika Angstroma w funkcji julian day
obszaru w niedalekim sasiedztwie
pustyni somalijskiej oraz cyrkulacja antycyklonalna w tym rejonie
sugeruja, ze dominowal tu aerozol organiczny oraz pyly piaskowe
naniesione wlasnie z tej pustyni. W kolejnych dniach, gdy statek
poruszal sie na poludnie grubosc optyczna oraz wykladnik
Angstroma ponownie rosly. W okolicach 5-go równoleznika
osiagnely one maksimum. AOT wynosila okolo 0.5 zas wykladnik
Angstoma 1.2. W rejonie wyzej wspomnianego równoleznika dolne
wiatry majace kierunek pólnocno wschodni transportuja ogromne
ilosci zanieczyszczen z centralnej i pólnocnej czesci Pólwyspu
Indyjskiego. Na poziomie 700 mb transport zanieczyszczen odbywa sie z obszaru poludniowych Indii. W
rezultacie prowadzi to do duzej kumulacji aerozolu w rozwazanym
obszarze. W kolejnych dniach statek utrzymywal swój kurs na
poludnie przecinajac równik i doplywajac do strefy zbieznosci
zlokalizowanej pomiedzy 10 a 12 stopniej szerokosci poludniowej. Grubosc
optyczna malala wraz z oddalaniem sie od Pólwyspu Indyjskiego.
Spadek ten byl monotoniczny i nawet po doplynieciu do ITCZ nie
zanotowano wzrostu koncentracji aerozolu. W obszarze najdalej
polozonym na poludnie AOT wynosila
0.1 (500nm). Podobnie jak w okolicach Mauritius tak i tu
wykladnik Angstroma byl niski, nawet po nizej 0.4. Za tak duzy
spadek odpowiedzialne sa chmury ci zwiazane z mezoskalowym
systemem konwekcyjnym zlokalizowanym w strefie zbieznosci. W
koncowej fazie tego etapu
badan grubosc optyczna aerozolu wzrosla i ustalila sie na
poziomie 0.5, który jest charakterystyczny dla okolic Male.
W trzecim czesci Indoex-u w
rejonie Zatoki Bengalskiej obserwowane bylo stopniowe
zmniejszanie sie AOT w czasie rejsu na wschód. W rejonie
równika byla ona najmniejsza okolo 0.2. Jednak dalej na pólnoc
ponownie obserwowany byl wzrost
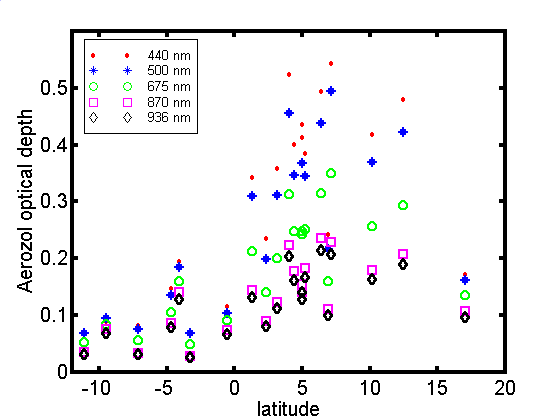
Wyk. 4.3 Grubosci
optyczna aerozolu w zaleznosci od szerokosci geograficznej.
grubosci optycznej. W tym rejonie
z reguly wialy slabe wiatry pólnocne, które nie mogly duzej
ilosci zanieczyszczen z obszarów poludniowej Azji. Bardziej
prawdopodobne wydaje sie, ze ich transport odbywal sie na wyzszym
poziomie czemu sprzyjala cyrkulacja antycyklonalna na powierzchni
700 mb. Równiez stosunkowo duza wartosc wykladnika Angstroma sugeruje, ze
wystepuje tu duzo malego aerozolu o podobnych wlasciwosciach
optycznych jak w rejonie Male.
Rozklad grubosci optycznej
aerozolu w zaleznosci od szerokosci geograficznej przedstawiony
jest na wyk. .Jest on podsumowaniem powyzej analizy. Zdecydowanie
najczystszym obszarem jest pólkula poludniowa z gruboscia
optyczna po nizej 0.05 (500nm). Nastepnie obserwujemy male
maksimum dla 4 równoleznika pólkuli poludniowej, gdzie AOT
osiaga wartosc 0.15 poczym ponownie zmniejsza sie. Maksimum to jest odzwierciedleniem
polozenia zbieznosci w tym okresie czasu. Po przekroczeniu
równika AOT gwaltownie wzrasta i osiaga wartosc najwieksza dla 5
stopnia szerokosci pólnocnej. W tym obszarze AOT wynosi okolo
0.5 (500nm). Dalej na pólnoc
grubosc optyczna wolno zmniejsza sie i rejonie 15 równoleznika
jest mniejsza od 0.2.
Mniej regularnie lecz wyraznie
zmienia sie wykladnik Angstroma. Najmniejsze wartosci byly
obserwowane na pólkuli poludniowej oraz na krancach pólnocnych
badanego obszaru. Jest to dowodem na to, ze koncentracja malego
aerozolu jest tam niewielka. Jednoczesnie rozklad spektralny AOT
wykazuje mniejszy spadek grubosci optycznej z dlugoscia fali niz
w przypadku gdy zawartosc malego aerozolu w powietrzu jest duza.
W wyzej wspomnianych
obszarach promieniowanie sloneczne jest
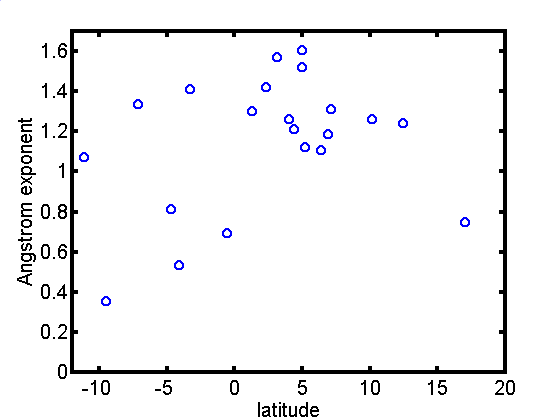
Wyk. 4.4 Wartosc
wykladnika Angstroma w zaleznosci od szerokosci geograficznej.
zdecydowanie silniej rozpraszane
do przodu w przeciwienstwie do regionu najbardziej
zanieczyszczonego, gdzie znaczna czesc promieniowania jest
rozpraszana do tylu. W okolicach 5 -go równoleznika na pólkuli
pólnocnej wykladnik Angstroma jest najwiekszy i wynosi 1.2-1.6.
Zatem grubosc optyczna maleje szybko ze wzrostem dlugosci fali.
Srednio dla dlugosci fal znajdujacych sie w bliskiej podczerwieni wynosi 0.2 podczas
gdy dla dlugosci fali równej 440nm jest blisko trzy razy
wiekszy.
Z wykresu 4.4 wynika, ze
wspólczynnik Angstroma w pojedynczych dniach spada bardzo
gwaltownie co jest spowodowane obecnoscia chmur ci subvisual w
obrebie mezoskalowych systemów konwekcyjnych. Obecnosc tego
rodzaju chmur jest dobrze widoczna na dobowych przebiegach AOT
oraz wspólczynnika Angstroma. Na wykresie 4.5 i 4.6 przedstawione sa takie przebiegi dla 76
jd, gdy statek znajdowal sie blisko strefy zbieznosci. Grubosc
optyczna gdy nie ma chmur ci jest rzedu 0.2 (500nm), jednak gdy
pojawia sie cirrus wartosc jej gwaltownie rosnie i wynosi
0.4-0.6. Tym samym spada wykladnik Angstroma do wartosci 0.2-0.3.
Dowodzi to, ze rozpraszajace czastki musza byc bardzo duze i moga byc to jedynie krysztalki lodu
w cirrusie. Wykres 4.5 i 4.6
ukazuje przebiegi obu tych wielkosci podczas 86 jd. Podczas
pomiarów wielkosci te utrzymuja sie na podobnym poziomie jednak
po 52 pomiarze AOT wzrasta dwukrotnie a wykladnik Angstroma
maleje z 1.5 do 0.6. Jest to kolejny ewidentny przyklad
pojawienia sie cirrusa slabo widocznego z powierzchni ziemi.
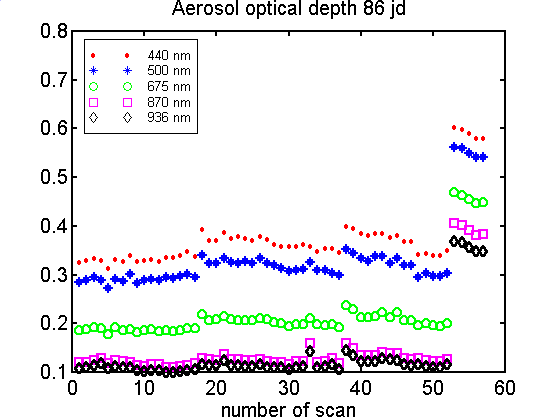
Wyk. 4.5 Zmiany
grubosci optycznej aerozolu w czasie dnia (86 jd)
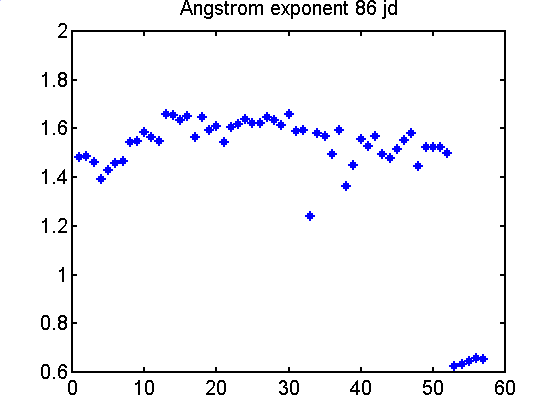
Wyk. 4.6 Zmiany
wykladnika Angstroma w czasie dnia (86 jd)
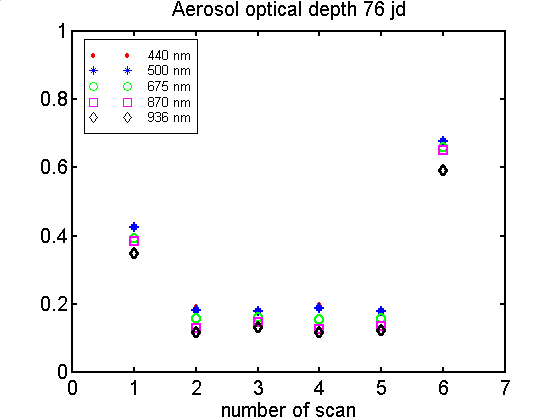
Wyk.4.7 Zmiany
grubosci optycznej aerozolu w czasie dnia (76 jd)
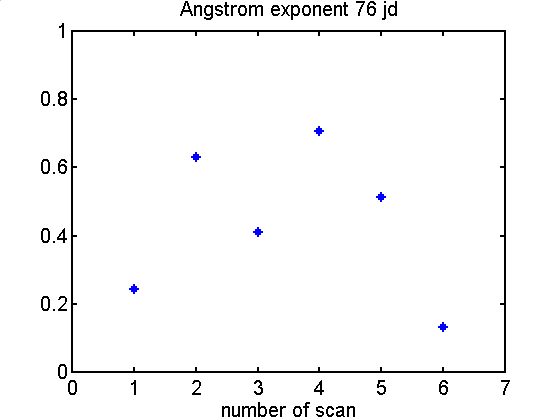
Wyk.4.8 Zmiany
wykladnika Angstroma podczas dnia (76 jd)
5. Kalibracja mikrotopsa- metoda
Langley’a.
W czasie przeszlo póltora
miesiecznego eksperymentu przeprowadzono dwa razy kalibracje
przyrzadu metoda Langley'a. Pierwsza wykonano 57 jd po poludniu
oraz druga 89 jd przeprowadzona w godzinach porannych.
Metoda Langley'a oparta jest na
pomiarach sygnalu dochodzacego do detektora przy róznych
polozeniach Slonca nad horyzontem w czasie stalych warunków
meteorologicznych. Szczególnie tyczy sie to niezmienniczosci AOT
oraz zawartosci pary wodnej w atmosferze. W czasie pomiarów
slonce nie moze byc przysloniete nawet cienkimi chmurami. Wymogi
te sa dosc trudne do zrealizowania szczególnie w tropikach, gdzie wystepuje duzo chmur typu
cirrus i cumulus. Pierwsza kalibracja wykonywana byla na pólkuli
poludniowej w obszarze, gdzie AOT byla niewielka. Prowadzona byla
przy praktycznie bezchmurnej pogodzie, jednak pod koniec
kalibracji wystapil wzrost zachmurzenia
blisko horyzontu. Druga kalibracja byla prowadzona rano,
rozpoczeta pól godziny po wschodzie slonca. Zachmurzenie
poczatkowo bylo niewielkie wystepowaly jedynie nieliczne cumulusy
na horyzoncie. Obserwowane bylo jednak znaczne zmetnienie, które ograniczalo widocznosc. W miare czasu
jednak zachmurzenie roslo pomimo tego slonce nie bylo przez nie
przyslaniane.
W przypadku mikrotopsa sygnal
wyjsciowy jest proporcjonalny do natezenia promieniowania dlatego
z prawa Beer’a otrzymujemy:
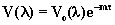 (5.1)
(5.1)
gdzie: Vo jest
sygnalem poza atmosfera
Uwzgledniajac zmiany odleglosci
Ziemi od Slonca oraz po zlogarytmowaniu obu stron otrzymujemy:
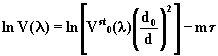 (5.2)
(5.2)
gdzie V0st
oznacza sygnal na górnej granicy atmosfery przy sredniej
odleglosci Ziemi od Slonca, zas d0 , d sa srednia i aktualna odlegloscia
Ziemi od Slonca.
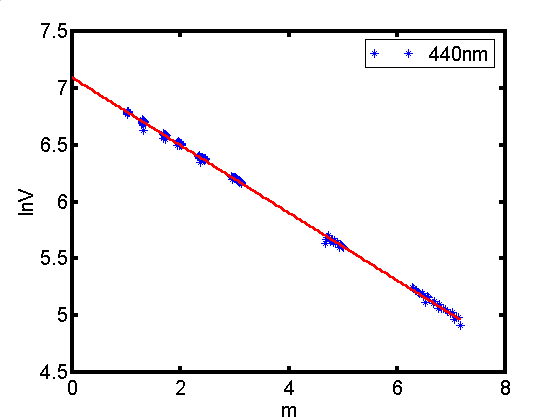
Wyk. 5.1
Kalibracja przyrzadu wykonana 57 julian day dla 440 nm
Powyzsze równanie jest liniowym
zwiazkiem pomiedzy logarytmem sygnal a masa optyczna. Wykonujac
pomiary przy róznych wartosciach masy optycznej atmosfery moza
okreslic parametry krzywej kalibracyjnej a nastepnie
ekstrapolujac ja do wartosci m=0 otrzymujemy poszukiwana wielkosc
V0st .
W celu dokladnego okreslenia tej prostej pomiary nalezy wykonywac
w czasie gdy masa optyczna zmienia sie istotnie w czasie. Taka
sytuacja wystepuje po wschodzie lub przed zachodem slonca. Nie
mozna jednak wykonywac kalibracji, gdy masa optyczna przekroczy
wartosc 10, poniewaz pomiary w tym czasie obarczone sa
najwiekszym bledem. Z drugiej strony powinno wykonywac jej przy
mozliwie najmniejszych katach
zenitalnych aby ekstrapolacja do masy optycznej równej zero byla
jak najbardziej dokladna. Jednak to znacznie wydluza proces
kalibracji, który powinien byc w miare krótki aby zapewnic
niezmienniczosc grubosci optycznej. W rezultacie pomiary kalibracyjne najlepiej prowadzic gdy kat
azymutalny zmienia sie w granicach od 45 do 800.
W przypadku kanalu 936 nm
równanie kalibracyjne jest nieco inne ze wzgledu na absorbcje
pary wodnej. Przyjmuje ono nastepujaca postac:
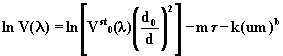 (5.3)
(5.3)
gdzie k, b sa stalymi zaleznymi
od charakterystyki optycznej filtru, u oznacza calkowita
zawartosc pary wodnej w atmosferze w [cm].
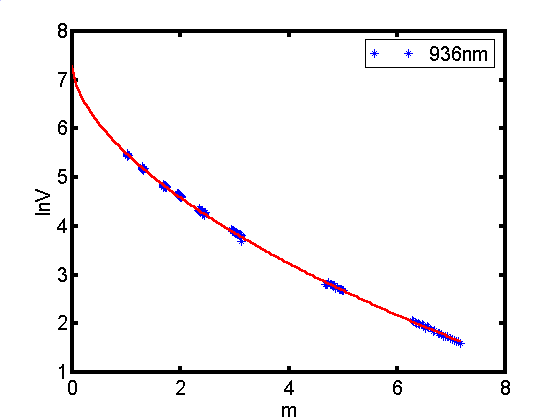
Wyk. 5.2 Kalibracja microtopsa wykonana 57
julian day dla 936nm
Metoda kalibracji w tym przypadku
jest identyczna jak dla wczesniejszych dlugosci fal róznica
polega jedynie na odmiennosci funkcji ekstrapolowanej. W tym
przypadku oprócz warunku stalosci grubosci optycznej wymagana
jest stalosc zawartosci pary wodnej. Ten drugi warunek jest
czesto nie do przyjecia ze wzgledu na znaczne zmiany tej
wielkosci podczas kalibracji. W celu poprawienia tej metody w
takich przypadkach przeprowadza sie regresje liniowa
uwzgledniajaca zmiany zawartosci pary wodnej. W ten sposób równanie 3 nieznacznie modyfikuje sie i
ma ostatecznie postac:
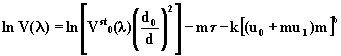 (5.4)
(5.4)
gdzie u0 oraz u1 okreslaja zmiany zawartosci pary wodnej w
czasie kalibracji.
Z przedstawionych danych w tabeli 5.1 wynika, ze przyrzad zachowywal sie dosc stabilnie
w czasie trwania Indoex-u.
Najwieksze róznice w stalych kalibracyjnych wystapily dla kanalu
440 nm. Odchylenia wartosci tych
stalych w stosunku do oryginalnych stalych kalibracyjnych wystepuja zarówno
w na plus jak i minus. Wobec czego przyjecie stalych kalibracyjnych uzyskanych w
czasie pomiarów na Hawajach w Mauna_Loa jest uzasadnione.
Tab. 5.1 Stale kalibracyjne
| Mauna_Loa lnV0
|
jd 057 lnV0
|
jd 089 lnV0
|
| 7.1070 |
7.0750 |
7.1211 |
| 6.8870 |
6.8708 |
6.9036 |
| 7.0540 |
7.0426 |
7.0651 |
| 6.6730 |
6.6712 |
6.6878 |
| 7.2580 |
7.2694 |
7.2445 |
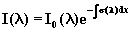 (3.1.1)
(3.1.1)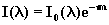 (3.1.2)
(3.1.2)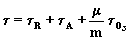 (3.1.3)
(3.1.3)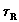 ,
, 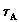 ,
, 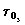 oznaczaja odpowiednio
grubosc optyczna: molekularna, aerozolowa oraz
ozonowa.
oznaczaja odpowiednio
grubosc optyczna: molekularna, aerozolowa oraz
ozonowa.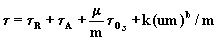 (3.1.4)
(3.1.4)
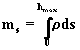 (3.2.2)
(3.2.2)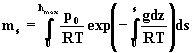 (3.2.3)
(3.2.3)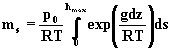 (3.2.4)
(3.2.4)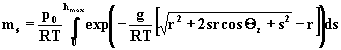 (3.2.7)
(3.2.7)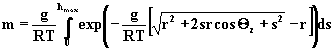 (3.2.9)
(3.2.9)
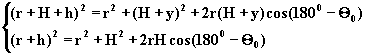 (3.2.13)
(3.2.13)
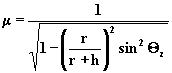 (3.2.17)
(3.2.17)









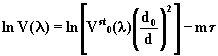 (5.2)
(5.2)
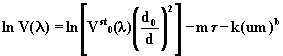 (5.3)
(5.3)
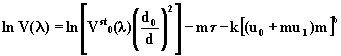 (5.4)
(5.4)